



Solve [ expr , vars ] attempts to solve the system expr of equations or inequalities for the variables vars .
Solve [ expr , vars , dom ] solves over the domain dom . Common choices of dom are Reals , Integers , and Complexes .




| lhs == rhs | equations | |
| lhs != rhs | inequations | |
| lhs > rhs or lhs >= rhs | inequalities | |
| expr ∈ dom | domain specifications | |
| < x , y , … >∈ reg | region specification | |
| ForAll [ x , cond , expr ] | universal quantifiers | |
| Exists [ x , cond , expr ] | existential quantifiers |
| no solutions | ||
| < < x ->sol x , y -> sol y , … > , … > | several solutions | |
| < < >> | solution set is full dimensional |
| Assumptions | $Assumptions | assumptions on parameters | |
| Cubics | Automatic | whether to use explicit radicals to solve all cubics | |
| GeneratedParameters | C | how to name parameters that are generated | |
| InverseFunctions | Automatic | whether to use symbolic inverse functions | |
| MaxExtraConditions | 0 | how many extra equational conditions on continuous parameters to allow | |
| MaxRoots | Infinity | maximum number of roots returned | |
| Method | Automatic | what method should be used | |
| Modulus | 0 | modulus to assume for integers | |
| Quartics | Automatic | whether to use explicit radicals to solve all quartics | |
| VerifySolutions | Automatic | whether to verify solutions obtained using non-equivalent transformations | |
| WorkingPrecision | Infinity | precision to be used in computations |
Solve a quadratic equation:
Solve simultaneous equations in  and
and 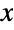 :
:
Solve an equation over the reals:
Solve an equation over the positive integers:
Solve equations in a geometric region:
Solutions are given as lists of replacements:
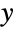
Use ReplaceAll ( /. ) to replace by solutions:
Check that solutions satisfy the equations:
Solve uses < >to represent the empty solution or no solution:
Solve uses < < >> to represent the universal solution or all points satisfying the equations:
Find solutions over specified domains:
Solve equations with coefficients involving a symbolic parameter:
Plot the real parts of the solutions for y as a function of the parameter a :
Solution of this equation over the reals requires conditions on the parameters:
Replace x by solutions and simplify the results:
Use Normal to remove the conditions:
Solution of this equation over the positive integers requires introduction of a new parameter:
List the first 10 solutions:
Polynomial equations solvable in radicals:
To use general formulas for solving cubic equations, set Cubics True :
By default, Solve uses Root objects to represent solutions of general cubic equations with numeric coefficients:
General polynomial equations:
Polynomial equations with multiple roots:
Find five roots of a polynomial of a high degree:
Polynomial equations with symbolic coefficients:
Solve cannot find all solutions here:
Find three solutions:
Univariate elementary function equations over bounded regions:
Univariate holomorphic function equations over bounded regions:
Here Solve finds some solutions but is not able to prove there are no other solutions:
Equation with a purely imaginary period over a vertical stripe in the complex plane:
Find a specified number of roots of an unrestricted complex equation:
Nonanalytic complex equations:
Systems of linear equations:
Linear equations with symbolic coefficients:
Underdetermined systems of linear equations:
Linear equations with no solutions:
Systems of polynomial equations:
Find five out of a trillion roots of a polynomial system:
Polynomial equations with symbolic coefficients:
Find a specified number of solutions of transcendental equations:
Square analytic systems over bounded boxes:
Polynomial equations with multiple roots:
Polynomial equations with symbolic coefficients:
Transcendental equations, solvable using inverse functions:
Transcendental equations, solvable using special function zeros:
Transcendental inequalities, solvable using special function zeros:
High-degree sparse polynomial equations:
Algebraic equations involving high-degree radicals:
Equations involving non-rational real powers:
Equation with a double root:
Tame elementary function equations:
Elementary function equations in bounded intervals:
Holomorphic function equations in bounded intervals:
Periodic elementary function equations over the reals:
Quantified polynomial systems:
Transcendental systems, solvable using inverse functions:
Systems exp-log in the first variable and polynomial in the other variables:
Systems elementary and bounded in the first variable and polynomial in the other variables:
Systems analytic and bounded in the first variable and polynomial in the other variables:
Square systems of analytic equations over bounded regions:
Linear systems of equations:
Linear systems of equations and inequalities:
Univariate polynomial equations:
Binary quadratic equations:
Sum of squares equations:
The Pythagorean equation:
Bounded systems of equations and inequalities:
High ‐ degree systems with no solutions:
Transcendental Diophantine systems:
Polynomial systems of congruences:
Univariate polynomial equations:
Systems of polynomial equations and inequations:
Quantified polynomial systems:
Systems of linear equations:
Systems of polynomial equations:
Mixed real and complex variables:
Mixed real and integer variables:
Solve over special regions in 2D:
Solve over special regions in 3D:
A quantified system:
An implicitly defined region:
A parametrically defined region:
Eliminate quantifiers over a Cartesian product of regions:
Regions dependent on parameters:
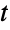
The answer depends on the parameter value :
Use 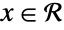 to specify that
to specify that 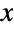 is a vector in
is a vector in 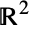 :
:
In this case 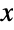 is a vector in
is a vector in 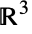 :
:
All variables are solved for:
Specify conditions on parameters using Assumptions :
By default, no solutions that require parameters to satisfy equations are produced:
With an equation on parameters given as an assumption, a solution is returned:
Assumptions that contain solve variables are considered to be a part of the system to solve:
Equivalent statement without using Assumptions :
With parameters assumed to belong to a discrete set, solutions involving arbitrary conditions are returned:
By default, Solve uses general formulas for solving cubics in radicals only when symbolic parameters are present:
For polynomials with numeric coefficients, Solve does not use the formulas:
With Cubics->False , Solve never uses the formulas:
With Cubics->True , Solve always uses the formulas:
Real roots of irreducible cubics still contain I in their algebraic forms by casus irreducibilis:
Machine-precision numerical evaluation gives a spurious imaginary part:
Arbitrary-precision evaluation still leaves an imaginary part:
With the default setting Cubics Automatic , explicitly real results are obtained:
Solve may introduce new parameters to represent the solution:
Use GeneratedParameters to control how the parameters are generated:
By default, Solve uses inverse functions but prints warning messages:
For symbols with the NumericFunction attribute, symbolic inverses are not used:
With InverseFunctions->True , Solve does not print inverse function warning messages:
Symbolic inverses are used for all symbols:
With InverseFunctions->False , Solve does not use inverse functions:
Solving algebraic equations does not require using inverse functions:
Here, a method based on Reduce is used, as it does not require using inverse functions:
By default, no solutions requiring extra conditions are produced:
Unless the parameters are discrete:
The default setting, MaxExtraConditions->0 , gives no solutions requiring conditions:
MaxExtraConditions->1 gives solutions requiring up to one equation on parameters:
MaxExtraConditions->2 gives solutions requiring up to two equations on parameters:
Give solutions requiring the minimal number of parameter equations:
Give all solutions:
By default, Solve drops inequation conditions on continuous parameters:
With MaxExtraConditions->All , Solve includes all conditions:
Find 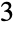 out of
out of 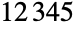 roots of a polynomial:
roots of a polynomial:
Find 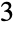 out of
out of 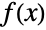 roots of a polynomial system:
roots of a polynomial system:
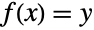
Find solutions of a transcendental system:
When the system contains symbolic parameters, the option value is ignored:
By default, Solve uses inverse functions to solve non-polynomial complex equations:
With Method->Reduce , Solve uses Reduce to find the complete solution set:
Solve equations over the integers modulo 9:
Find a modulus for which a system of equations has a solution:
By default, Solve uses the general formulas for solving quartics in radicals only when symbolic parameters are present:
For polynomials with numeric coefficients, Solve does not use the formulas:
With Quartics->False , Solve never uses the formulas:
With Quartics->True , Solve always uses the formulas:
Solve verifies solutions obtained using non-equivalent transformations:
With VerifySolutions->False , Solve does not verify the solutions:
Some of the solutions returned with VerifySolutions->False are not correct:
This uses a fast numeric test in an attempt to select correct solutions:
In this case numeric verification gives the correct solution set:
By default, Solve finds exact solutions of equations:
Computing the solution using 100-digit numbers is faster:
The result agrees with the exact solution in the first 100 digits:
Computing the solution using machine numbers is much faster:
The result is still quite close to the exact solution:
Solve a quadratic equation:
Find intersection points of a circle and a parabola:
Find conditions for a quartic to have all roots equal:
A method using quantifier elimination:
Plot a space curve given by an implicit description:
Plot the projection of the space curve on the < x , y >plane:
Find a Pythagorean triple:
Find a sequence of Pythagorean triples:
Find how to pay $2.27 postage with 10-, 23-, and 37-cent stamps:
The same task can be accomplished with IntegerPartitions :
Find 200 roots of a complex analytic function:
Show the roots on the complex plot for the function:
Solutions satisfy the equations:
Solutions are given as replacement rules and can be directly used for substitution:
Solve uses < >to represent the empty solution or no solution:
Solve uses < < >> to represent the universal solution or all points satisfying the equations:
For univariate equations, Solve repeats solutions according to their multiplicity:
Solutions of algebraic equations are often given in terms of Root objects:
Use N to compute numeric approximations of Root objects:
Root objects may involve parameters:
Use Series to compute series expansions of Root objects:
The series satisfies the equation up to order 11:
Solve represents solutions in terms of replacement rules:
Reduce represents solutions in terms of Boolean combinations of equations and inequalities:
Solve uses fast heuristics to solve transcendental equations, but may give incomplete solutions:
Reduce uses methods that are often slower, but finds all solutions and gives all necessary conditions:
Use FindInstance to find solution instances:
Like Reduce , FindInstance can be given inequalities and domain specifications:
Use DSolve to solve differential equations:
Use RSolve to solve recurrence equations:
SolveAlways gives the values of parameters for which complex equations are always true:
The same problem can be expressed using ForAll and solved with Solve or Reduce :
Resolve eliminates quantifiers, possibly without solving the resulting quantifier-free system:
Eliminate eliminates variables from systems of complex equations:
This solves the same problem using Resolve :
Reduce and Solve additionally solve the resulting equations:
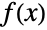 is bijective iff the equation
is bijective iff the equation 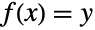 has exactly one solution for each
has exactly one solution for each 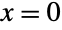 :
:
Use FunctionBijective to test whether a function is bijective:
Use FunctionAnalytic to test whether a function is analytic:
An analytic function can have only finitely many zeros in a closed and bounded region:
Solve gives generic solutions; solutions involving equations on parameters are not given:
Reduce gives all solutions, including those that require equations on parameters:
With MaxExtraConditions->All , Solve also gives non-generic solutions:
Solve results do not depend on whether some of the input equations contain only parameters. The following two systems are equivalent and have no generic solutions:
Use MaxExtraConditions to specify the number of parameter conditions allowed:
Use the Exists quantifier to find solutions that are valid for some value of parameter :
Solve does not eliminate solutions that are neither generically correct nor generically incorrect:
The solutions are correct for 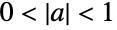 and incorrect for
and incorrect for 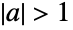 :
:
For transcendental equations, Solve may not give all solutions:
Use Reduce to get all solutions:
Solve with Method->"Reduce" uses Reduce to find solutions, but returns replacement rules:
Using inverse functions allows Solve to find some solutions fast:
Finding the complete solution may take much longer, and the solution may be large:
This finds the values of n for which x ==2 is a solution:
Interpretation of assumptions depends on their syntactic properties. Here the solution is generic in the parameter space restricted by the assumptions:
This mathematically equivalent assumption contains the solve variable, and hence is treated as a part of the system to solve:
There are no generic solutions, because the input is interpreted as:
The solution is non-generic, since it requires the parameters to satisfy an equation:
When parameters are restricted to a discrete set, the notion of genericity is not well defined, and all solutions are returned:
Removable singularities of input equations are generally not considered valid solutions:
However, solutions may include removable singularities that are cancelled by automatic simplification:
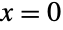
The removable singularity at is cancelled by evaluation:
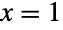
Here the removable singularity at is cancelled by Together , which is used to preprocess the equation:
The value of MaxRoots is used only for systems with numeric coefficients:
When symbolic parameters are present, the option value is ignored:
Expressions given as variables are treated as atomic objects and not as functions of their subexpressions:
Effectively, variables are replaced with new symbols before the equations are solved:
The result comes from:
Introduced in 1988 (1.0) | Updated in 1996 (3.0) ▪ 2014 (10.0) ▪ 2020 (12.2) ▪ 2024 (14.0)